Saugverhalten von Kreiselpumpen

 

H_A =      +             + H_geo +

H_Vs + H_Vd in [m]⇥(1)

p_a, p_e statische Drücke in [Pa]

ρ Fluiddichte in [kg/m³]

g Erdbeschleunigung mit 9,81 m/s²

c_a, c_e Geschwindigkeit im Behälter in [m/s]

H_geo ≈ Ha – He geodätische Höhe in [m]

H_Vs, H_Vd Saug- bzw. Druckverluste in [m]

 

Die allgemeinen Druckverluste errechnen sich aus:

H_V = ( x l + Σξ) x        in [m]

λ Rohrreibungszahl

l Rohrlänge in [m]

d Rohrdurchmesser in [m]

ξ Widerstandsbeiwerte von Formstücken und Einbauten
(Armaturen, usw.)

c Strömungsgeschwindigkeit im Rohr in [m/s]

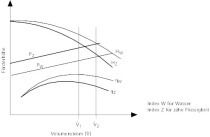
H_v = f(V) mit c =       ,

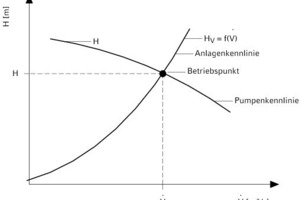
wobei A der durchströmte Querschnitt ist, so dass H_V = Konstante x V² mit V als Volumenstrom in [m³/s] (Bild 2).

Somit ist der Förderhöhe der Anlage H_A im Betriebspunkt identisch der „Pumpenförderhöhe H“

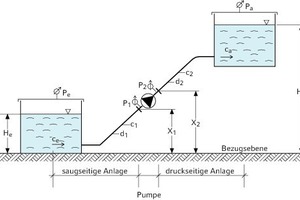
H_A = H =            +          + (x₂ – x₁) in [m] ⇥(2)

 

Vernachlässigt man x₂ – x₁ (= Manometerabstand), und setzt c₁ = c₂ bei d₁ = d₂ so wird

H_A = H = = in [m]⇥(3)

und der Leistungsbedarf an der Welle

Pw = in [J/s] = [W]⇥(4)

Δp_V Druckverlust in [Pa]

V Fördervolumenstrom in [m³/s]

η Pumpenwirkungsgrad

 

Saugverhalten und Haltedruckhöhe

Um Zerstörungen am Laufrad und seiner Umgebung sowie Betriebsstörungen durch „Kavitationserscheinungen“ zu vermeiden, dürfen Grenzwerte der Ansaugbedingungen von Kreiselpumpen nicht unterschritten werden. Hierfür sind die „Haltedruckhöhe H_HA“ oder „NPSH-Wert“ wichtige Begriffe.

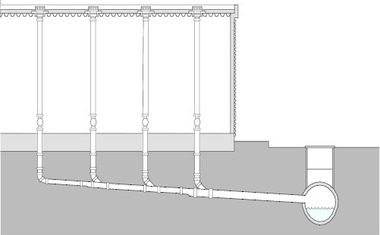
Zur Einführung bezüglich des „Saugverhaltens“
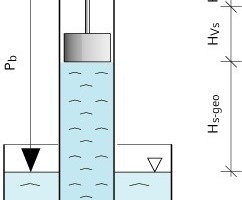
(Bild 3):

Eine Kolbenpumpe kann bekanntlich Wasser aus Tiefen bis etwa 9 m ansaugen, wenn auf dem Saugspiegel ein Atmosphärendruck von 1 bar liegt. Wird der Kolben angehoben, dann entsteht im Rohr unterhalb des Kolbens ein Unterdruck (Vakuum) und der Atmosphärendruck drückt das Wasser im Rohr nach oben. Je langsamer der Kolben bewegt wird, umso höher steigt die Wassersäule (H_s-geo). Der Atmosphärendruck p_b hat aber nicht nur H_s-geo das Gleichgewicht zu halten, er muss auch alle bei der Bewegung des Wassers auftretenden Widerstände H_v-s überwinden.

Außerdem ist der Druck unter dem Kolben nicht Null, weil das Wasser bei jeder Temperatur gesättigte Dämpfe ausscheidet, deren Druck p_D gemäß Dampfdruckkurve temperaturabhängig ist (z. B. Wasser von 15 °C hat einen p_D = 0,017 bar, das entspricht 0,017 x 105 Pa/(ρ x g) = 0,17 m = H_D). Da dem Wasser im Rohr die Geschwindigkeit c_s erteilt wurde, ist die dafür erforderliche Geschwindigkeitsenergie oder Geschwindigkeitshöhe c_s²/2g vom Atmosphärendruck aufzubringen.

So lautet die Bilanz:

H_s-geo = – H_Vs – H_D – c_s²/2g in [m]⇥(5)

 

Grundsätzlich gelten für Kreiselpumpen die gleichen Überlegungen. Hier sind jedoch die Verhältnisse schwieriger, einmal weil es den „dichten Kolben“ nicht gibt, außerdem weil größere vom Förderstrom abhängige Strömungsgeschwindigkeiten in den verschiedenen wesentlichen Querschnitten der Anlage und der Pumpe herrschen.Das Saugverhalten einer Kreiselpumpe wird durch Kavitation in der saugseitigen Pumpenanlage und in der Pumpe selbst bestimmt. Als Kavitation bezeichnet man die Bildung und das Zusammenfallen von Dampfblasen in strömenden Flüssigkeiten.

Die Dampfblasen bilden sich an Stellen, an denen der Druck auf den zu der Temperatur der Flüssigkeit gehörenden Dampfdruck sinkt.

Die Kavitationsentstehung nach dem 1. Hauptsatz der Thermodynamik

Die saugseitig auftretenden Strömungswiderstände H_Vs in den Gleichungen (1) und (5) in Rohrleitungen, Armaturen, Einbauten etc. im Anlagennetz werden mit

H_V = ( x l + Σξ) x bzw. Δp_V = ( x l + Σξ) x ρ/2 x c²

 

erfasst und sind eine Funktion des Volumenstrom V.

Diese Strömungswiderstände sind ungewollte „Drosselungen“, während Drosselungen in Druckminderventilen und Reduzierstationen gewollt sind.

Drosselungen sind irreversible Strömungsprozesse, die durch Reibung entstehen, bei denen Entropie produziert wird, womit ein Exergieverlust einhergeht.

Nun gilt allgemein für „stationäre Fließprozesse“ der 1. Hauptsatz der Thermodynamik: (1 2)

Q₁₂ + P₁₂ = m [(h₂-h₁) + ½ (c₂² – c₁²) + g (z₂ – z₁)]

P₁₂ = m x w_t-12

 

oder in differentieller Schreibweise

 

dq +dw_t = dh + c x dc + g x dz

 

Da es sich hier um adiabatische (Q = 0) Strömungsprozesse handelt, entfällt auch die technische Arbeit (P = 0) bzw. Leistung sowie die potentielle Energie g x z, so dass:

 

h₁ + c₁²/2 = h₂ + c₂²/2

 

wird und werden die Querschnitte so bemessen, dass c₁ = c₂, so ergibt sich:

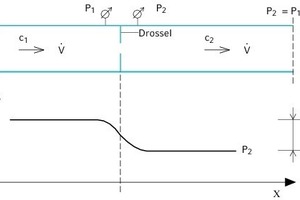
h₁ = h₂, und der Drosselungsprozess findet bei konstanter Enthalpie statt. Diese isenthalpe Zustandsänderung setzt voraus, dass die Geschwindigkeitsenergie (oder kinetische Energie) vernachlässigt werden kann (Bild 4).

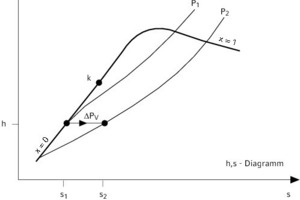
Der isenthalpe Zustandsverlauf der Drosselung erfolgt in Dampf-Diagrammen von Wasser (oder sonstiger flüssiger Fluide z. B. Kältemitteln) bzw. h,s-Diagramm bei einer Linie h = konstant waagrecht, im log p,h-Diagramm senkrecht.

Man erkennt: Aus gesättigter Flüssigkeit entsteht z. B. ein Wasser-Dampf-Gemisch (Nassdampf) (Bild 5).

Aus Gleichung (2) ersieht man den statischen und den dynamischen Druckanteil am Gesamtdruck der Anlage (Bild 1, z₁, z₂ vernachlässigt):

 

p_ges = p₂ – p₁ + ρ/2 x ( – )

p_ges = p_stat + p_dyn

 

p_stat ist der überwiegende Teil bei dem Druckerhöhungsprozess in der Pumpe, der auf der Rohrwand messbar ist. Erst beim Vorhandensein einer Fluidgeschwindigkeit wird das Druckpotential in Bewegungsenergie (kinetische Energie) umgewandelt.

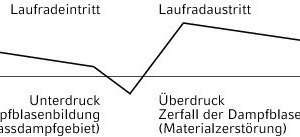
Bilanziert man die Änderung der Druckanteile im Verlauf eines Strömungsprozesses, so wird der statische Druckanteil immer weiter abnehmen und sukzessive in dynamischen Druck umgesetzt. Zusammengefasst ergibt sich: Der am Laufradeintritt noch zur Verfügung stehende statische Druck sollte um einen Sicherheitsfaktor größer sein als der temperaturabhängige Wasserdampfteildruck (Bild 6). Kavitation kann also nur in be­schränktem Ausmaß zugelas­sen werden, denn die Folge sind ein Abfall der Förderhöhe und des Wirkungsgrades bis zum Abreißen der Förderung, Geräusche, Laufunruhe und „Anfressungen“ am Laufrad und anderen Pumpeninnenteilen.

Bezeichnet man in der v.g. Gleichung H_s-geo^max als z₁^max, so ist dies die maximal zulässige Aufstellhöhe der Pumpe:

z₁^max = – (H_Vs + ) = H_HA^max = max. Haltedruckhöhe

in [m] ⇥(6)

p_b = atmosphärischer Luftdruck in [Pa]

p_D = Flüssigkeitsdampfdruck bei t in [°C] in [Pa]

H_Vs = saugseitiger Druckverlust in [m]

c_s = Sauggeschwindigkeit in [m/s]

Bei gegebener Aufstellungshöhe z₁ (Bild 1) ergibt sich die vorhandene Haltedruckhöhe H_Ha^vorh

H_HA^vorh = z₁^max – z₁ = NPSH_vorh⇥(7)

oder

H_HA^vorh = NPSH_vorh = – (H_Vs + c_s²/2g + z₁)

Nun hat die „Kreiselpumpe“ ihren eigenen NPSH-Wert der NPSH_erforderlich genannt wird:

 

NPSH_erforderlich = (0,3 bis 0,5) x n /¯ V in [m], wenn n = 10 -> 50 s^-1 und V = 0,1 ≥ 1 m³/s sind.

 

In der Regel wird der NPSH_erforderlich vom Pumpenhersteller angegeben. Nun gilt:

 

NPSH_vorh ≥ NPSH_erf⇥(8)

 

Ein Beispiel:

a) Aus einem offenen Brunnen wird über eine Kreiselpumpe Wasser angesaugt. Aufstellungshöhe der Pumpe z₁ = 3 m über dem Wasserspiegel. p_b = 1 bar, H_D = 0,23 m, H_Vs = 0,95 m, c_s = 2 m/s, gesucht wird die Haltedruckhöhe H_HA^vorh

H_HA^vorh = NPSH_vorh = – (H_D + z₁ + H_Vs + c_s²/2g) = 10 m –

– (0,23 + 3 + 0,95 + 0,2) m = 5,62 m

 

b) Wie groß ist H_HA^vorh, wenn anstelle des Brunnens aus einem höher liegenden offenen Behälter mit z₁ = 3 m Zulaufhöhe angesaugt wird?

H_HA^vorh = NPSH_vorh = + z₁ – (H_D + H_Vs + ) =

= 10 m + 3 m – (0,23 + 0,95 + 0,2) m = 11,65 m

 

Anmerkung:

Aus Gleichung (8) erkennt man, dass je kleiner der NPSH_vor wird, desto geringer ist die Gefahr der Kaviation. Nun können Pumpen nicht nur nach dem Gesichtspunkt möglichst kleinem NPSH_vor konstruiert werden. Zwei verschiedene Pumpen können also bei gleichem Förderstrom, Förderhöhe und Drehzahl sehr verschiedene NPSH_vor haben.