Die Vernetzung der Energie mit Entropie und Exergie

Zitat: „Niemand weiß so genau wie Quantenmechanik funktioniert, und niemand weiß, was Energie ist.“

Richard Feynman (1918 bis 1988, Nobelpreisträger für Physik)

Es gibt eine Erfahrung, die jeder macht: „Es gibt in der Natur und in der Technik keinen Prozess der sich vollständig rückgängig machen lässt“ oder „Alle natürlichen (wirklichen) Prozesse sind irreversibel (nicht umkehrbar)“. Daraus kann man umgekehrt folgern: „Reversible (umkehrbare) Prozesse sind idealisiert jene, an denen man die Güte der irreversiblen Prozesse der technischen Anlagen und ihrer Komponenten bewerten kann.“

Während sich die Energieform „Arbeit“ (mechanisch, potentielle, kinetische, elektrische Arbeit) vollständig in die Energieform „Wärme“ umwandeln lässt, lässt sich diese „Wärme“ niemals ganz in „Arbeit“ umwandeln (oder nach Max Planck: „Alle Prozesse, bei denen Reibung auftritt, sind irreversibel“).

Die Umwandlung dieser beschränkt umwandelbaren Energieform „Wärme“ wird von der „Umgebung“ mit der Umgebungstemperatur T_u beeinflusst. Diese bei einem technischen Prozess auftretende „Umgebung“ als „Bezugssystem“ ist die „irdische Atmosphäre“; denn sie nimmt an den Energieumwandlungsprozessen auf der Erde als ein großer Energiespeicher teil, der Energie aufnehmen oder abgeben kann, ohne seinen intensiven Zustand zu verändern.

Würde sich die in der Umgebung gespeicherte (i.M. global ca. +15 °C = 288 K) Wärme in „Nutzarbeit“ umwandeln lassen, so wäre dies die ideale Energiequelle und es gäbe für die Menschheit keine Energieprobleme mehr.

Alle wirklichen Prozesse die „anfangs“ eine höhere Temperatur und einen höheren Druck als die Umgebung haben, streben nur in eine Richtung, nämlich zum thermischen und mechanischen Gleichgewicht mit der Umgebung.

Eine andere Richtung ist nie beobachtet worden. Eine Umkehr ist nicht möglich und die „innere Energie“ der Umgebung ist nicht in „Nutzarbeit“ zu verwandeln.

Aber alle technischen Prozesse die das menschliche Leben möglich machen, wie das Heizen, Kühlen, Produzieren, die Mobilität etc. brauchen keine Energie schlechthin, sondern Nutzarbeit, also die hochwertigere Energieform als die niederwertige Energieform der Umweltenergie.

Beispiel: 1 kg Wasser wird bei konstantem Druck (dp = 0) einmal von der Umgebungstemperatur von 20 °C (T_u = 293 K) auf 50 °C (T₁ = 323 K) und einmal von 50 °C auf 80 °C (T₂= 353 K) erwärmt.

Wie groß ist

a) die jeweilige zuzuführende Wärmeenergie?

b) wie ist diese zu bewerten?

zu a) Nach dem 1. Hauptsatz der Thermodynamik (oder allgemein Energiesatz) ist die zuzuführende Wärmemenge Q₁:

Q₁ = m x c_w x (T₁ – T_u) (1)

m = Masse in [kg]

c_w = spezifische Wärmekapazität von Wasser 4,19 kJ/kg K

Q₁ = 1 x 4,19 x (323 -293) kJ = 125,7 kJ

und

Q₂ = m x c_w x (T₂ – T₁) = 1 x 4,19 x (353 -323) kJ = 125,7 kJ

Ergo: Q₁ = Q ₂

Beide Wärmemengen sind nach dem 1. Hauptsatz gleich!

Denn der 1. Hauptsatz sagt: Keine Energie geht verloren, sondern die Energie wird von einer Energieform in eine andere Energieform umgewandelt, d.h. die Energie ist konstant!

Anmerkung: Einleuchtend ist jedoch, dass eine Wärme mit der mittleren Temperatur von

tm₂ = = 65 °C

höher zu bewerten ist, als eine Wärme mit der mittleren Temperatur von

tm₁ = = 35 °C

Darüber macht der 1. Hauptsatz keine Aussage.

Anmerkung: die mittlere arithmetische Temperatur tm₁ bzw. tm₂ weicht bei niedrigen Temperaturen etwas von der mittleren thermodynamischen Temperatur Tm₁ bzw. Tm₂ ab, wie anschließend gezeigt wird. In der Thermodynamik wird zudem grundsätzlich mit der Kelvin-Temperatur gerechnet.

Nun rechnet man im oben gezeigten Beispiel anstelle der Temperaturdifferenzen (T₁ – T_u) bzw. (T₂ – T₁) mit der mittleren thermodynamischen Temperatur T_m , so ergibt sich für:

Q₁ = m x c_w x (T₁ – T_u) = Q₂ = m x c_w x (T₂ – T₁) = Q

Q₁ = T_m1 x ? bzw. Q₂ = T_m2 x ?

und es fehlt eine Zustandsgröße. Man führt also eine neue „Zustandsgröße“ ein, die man „Entropie“ (S) nennt und man erhält:

Q= m x c_w x (T₁ – T_u) = T_m1 x (S₁ – S_u)

= m x c_w x (T₂ – T₁) = T_m2 x (S₂ – S₁)

1. Hauptsatz 2. Hauptsatz

S_u = Entropie im Umgebungszustand in [KJ/K] (s_u= spezifische Entropie in [KJ/kg K])

S₁ bzw. S₂ = Entropie im Zustand 1 bzw. 2 in [KJ/K] und als Differential­gleichung:

dQ = m x c_w x dT = T x dS(2)

und umgestellt:

dS = m x c_w x

und zwischen Zustand 1 und 2:

S₁₂ = ∫ m x c_w x = m x c_w x ln T₂/T₁

 
und daraus ergibt sich die thermodynamische Mitteltemperatur:

Q = m x c_w x (T₂ – T₁) = T_m2 x S₁₂ = T_m2 x m x c_w x ln T₂/T₁

Was im Beispiel zu:

T_m2 = 337,78 K (t_m2 = 337,78 K – 273 K = 64,78 °C)

T_m1 = 307,76 K (t_m1= 307,76 K – 273 K = 34,76 °C)

führt.

Man kann nun mit dem 2. Hauptsatz rechnen wie mit dem 1. Hauptsatz.

Die jeweilige Entropie im Beispiel wird dann zu:

S_1u = 1 x 4,19 x ln 323/293 kJ/kg = Q/T_m1 = 0,4084 kJ/K

und

S ₁₂ = 1 x 4,19 x ln 353/323 kJ/K = Q/T_m2 = 0,372 kJ/K

Jetzt hat man eine Bewertung der Wärmeenergie (die nach dem 1. Hauptsatz gleich ist):

„Je kleiner die Entropie desto hochwertiger ist die Wärme bei der Umwandlung in „technische Arbeitsfähigkeit““.

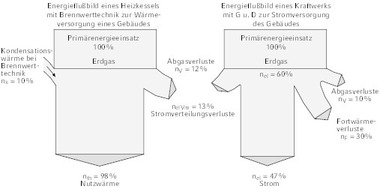
Denn Arbeit (p x dV oder V x dp) wie die mechanische, kinetische, potentielle, elektronische, etc. hat keine Entropie (gemäß Bild 1).

Q = (T_m1 – T_u) x S_1u + T_u x S_1u

(3)

E_Q1                         B_Q1

Q = (T_m2 – Tu) x S₁₂ + T_u x S₁₂

E_Q2                        B_Q2

E_Q = Exergie (technische Arbeitsfähigkeit)

B_Q = Anergie (Umweltenergie)

Nun hat man gemäß dem oben genannten die Aussage

Energie = Exergie + Anergie(4)

Jede Energie besteht also aus Exergie und Anergie, wobei einer der beiden Anteile auch Null sein kann. Zum Beispiel ist die Anergie = 0, dann ist die Exergie = 100 % = technische Arbeitsfähigkeit (wie E_pot, E_kin, E_elekt, etc.): ist die Exergie = 0 dann ist die Anergie = 100% Umweltwärme (z. B. durch die Sonnenstrahlung erhält die Erde negative Entropie und bis zu 95 % Exergie).

Der Energiebegriff des Energietechnikers deckt sich daher mit dem Exergiebegriff, nicht mit dem Energiebegriff des 1. Hauptsatzes.

Energieverbrauch und Energieverlust sind Begriffe die dem 1. Hauptsatz widersprechen, denn Energie kann nicht verbraucht werden und kann nicht verloren gehen.

Diese Begriffe werden jedoch sinnvoll für die Exergie, die bei allen technischen Prozessen, die alle irreversibel sind, unwiederbringlich in Anergie umgewandelt werden, also so genannte Exergieverluste!

Um nun den Anteil der Exergie in der Wärme zu ermitteln, bedient man sich nachfolgender Ableitung (gemäß Bild 1):

E_Q =Q – B_Q = Q – T_u x ΔS mit ΔS = Q/T_m(5)

E_Q =Q – Tu x Q_m; T_m = Q (1 – T_u/T_m) = Q x η_c mit η_c als Carnotfaktor

In unserem Beispiel ist der Exergieanteil:

E_Q1 = η_c1 x Q₁ = 125,7 x (1 – 293/307,76) kJ = 6,03 kJ und

E_Q2 = η_c2 x Q₂ = 125,7 x (1 – 293/337,78) kJ = 16,66 kJ

und der Anergieanteil:

B_Q1 = T_u x S_1u = 293 x 0,4084 kJ = 119,66 kJ

B_Q2 = T_u x S₁₂ = 293 x 0,3721 kJ = 106,03 kJ

oder: B_Q = Q - E_Q

Zu bedenken ist jedoch, dass Q₂ von einer höheren Anfangstemperatur begonnen hat, d.h. von einer Anfangsexergie ausging.

Beispiel: Aufheizen einer Flüssigkeit mit c_F = 1,0 kJ/kg K, dp = 0

a) einmal von T_U = 300 K auf T₁ = 600 K

und

b) einmal von T₁ = 600 K auf T₂ = 900 K

Welche spezifische Entropie und welche spezifische Exergie treten je auf?

zu a) s_1u = 1,0 x ln 600/300 kJ/kg K = 0,693 kJ/kg K

bei q = c_F x (T₁ – T_u) = 1,0 x 300 kJ/kg = 300 kJ/kg

e_q1 = 300 (1 – 300/432,8) kJ/kg = 92 kJ/kg, also 31 % Exergie

zu b) s₁₂ = 1,0 x ln 900/600 kJ/kg K = 0,406 kJ/kg K

e_q2 = 300 (1 – 300/740) kJ/kg = 178,4 kJ/kg, also 60 % Exergie

Bei gleicher Wärmemenge ist die Exergie größer, je kleiner die Entropie ist!

In der Technik – die vorwiegend als „offene Systeme“ behandelt werden – wird eine Masse m von Zustand 1 (mit p₁) zum Zustand 2 (mit p₂) transportiert. Dafür wird die Druckdifferenz (p₁ – p₂) benötigt um die Reibung zu überwinden (irreversibler Prozess) so dass der 1. Hauptsatz für Strömungs- oder Fließprozesse (stationär)

q + ∫ v x dp = h₂ – h₁(6)

ist.

h = spezifische Enthalpie in kJ/kg = Wärme q + Verschiebearbeit v x dp

Anmerkung für die Praxis: bei flüssigen Fluiden ist v = const. d.h.

h₂ – h₁ = q+v x (p₁ – p₂);

und die Entropie hängt nur von der Temperatur ab:

s₁₂ = ∫ c_F x dT/T = c_F x ln T₂/T₁(7)

 
bei gasförmigen Fluiden ist v ≠ const. und die spezifische Entropie

s₁₂=c_p x ln T₂/T₁ – R x ln P₂/P₁(8)

R = Gaskonstante

Beispiel:

a) Welche Exergie muss man 1 kg Wasser von T_u = 15 °C auf T = 100 °C zuführen

(c_w = 4,19 kJ/kg K, dp = 0) und wie groß die die Entropieproduktion bei dem Aufheizvorgang?

b) Welcher Exergieverlust (= Arbeitsverlust) tritt auf, wenn das Wasser (siedend) auf T_u = 15 °C wieder abkühlt und welche Entropieproduktion bei dem Abkühlvorgang?

c) Welche zeitliche Änderung (k-Wert: k x A = 0,75 W/K der diathermen Wand) der Wassertemperatur T, der Entropie vom Wasser und der Umgebung bei der Abkühlung?

zu a) Mit der bei dem Temperaturintervall (siehe Bild 2) aufgenommene Wärmemenge dQ nimmt das Arbeitsmedium Wasser die Entropie

dS_Q = dQ/T_m auf als Entropieproduktion

Q_zu = m x c_w x (T–T_u) = 1,0 x 4,19 (373 - 288) kJ = 356,15 kJ

S_ua = m x c_w x ln T/Tu = 1,0 x 4,19 x ln 373/288 kJ/K = 1,084 kJ/K

= Q/T_m = 356,15/328,67 kJ/K = 1,084 kJ/K

E_Q = m x c_w x (T – Tu) – Tu (S_Q - S_u) = (1,0 x 4,19 (373 – 288) – 288 x 1,084) kJ = 44 kJ 

= Q x η_c = 356,15 (1 – 288/328,67) kJ = 44 kJ

Die Anergie der Wärme ergibt sich aus dem Produkt der Umgebungstemperatur T_U und der mit der zugeführten Wärme dQ transportierten Entropie dS_UQ.

zu b) Wird nun die Wärme (siehe Bild 3) in einem Temperaturintervall vom Wasser an die Umgebung wieder abgegeben bzw. der Umgebung zugeführt, so ist die abgegebene Wärme Q_ab = m x c_w (T–T_u) = Q_zu= 356,15 kJ und die abgegebene Exergie E_Q gleich der zugeführten Exergie bei der Wärmeaufnahme des Wassers.

Nun verwandelt sich wie bei allen irreversiblen Prozessen letztlich die Exergie in Anergie!

D.h. im gezeigten Beispiel wird die dem Wasser zugeführten Exergie E_Q bei der Abkühlung ein Exergieverlust E_V(= Arbeitsverlust).

Da nach dem 1. Hauptsatz keine Energie verloren geht und der intensive Umgebungszustand unverändert bleibt, wird der Exergieverlust E_v zu Anergie und zu einer zusätzlichen Entropieproduktion, die man S_irr nennt.

S_irr = E_Q/T_u = E_V/T_u = 44/288 kJ/K = 0,153 kJ/K

und E_v = T_u x S_irr = 288 x 0,153 kJ = 44 kJ

oder

S_irr = S_u – S_Q = Q/T_u – Q/T_m = 356,15/288 – 356.15/328,67 = 1,236 – 1,084 = 0,153 kJ/K

Bei allen wirklichen Prozessen auf der Erde wird Exergie letztlich zur Anergie und der Exergieverlust wird in Entropie umgewandelt und erhöht die Gesamtentropie auf dem Planeten.

D.h. Energie ist mit Entropie und Exergie vernetzt mit dem Bezugs-System der Umgebung.

Diese allgemeinen Zusammenhänge zwischen E_V und S_irr zeigt die praktische Bedeutung bei der Planung energietechnischer Anlagen.

Zu c) Zeitliche Änderung der Temperatur (siehe Bild 4):

dQ/dt = – Q = – k x A x (T –T_u)

dQ = m x c_w x dT = - k x A x (T – T_u) dt

Durch Integration ergibt dies:

∫ dT/(T – Tu) = ∫ - x dt

ln = - x t

e                    =

z. B. nach t = 5 h ergibt sich dann:

-

T = ((373 – 288) x e                                     + 288) K = 291,4 K

Nach ca. 8 h ist praktisch die Umgebungstemperatur T_u = 288 K erreicht.

Zeitliche Änderung der Entropie

1) mit der an die Atmosphäre übergehende Wärme wird auch Entropie abgeführt, so dass S_Q abnimmt:

dS_Q = - = m x c_w x dT/T und zwischen t = 0 entsprechend

T = T₀ und einer beliebigen Zeit t zu der die Wassertemperatur den Wert T(t) hat, erhält man

S_Q(t) = S_Q (0) + m x c_w x ln T(t)/T₀

2) Die Entropie der Umgebung S_U nimmt zu, weil ihr mit der zugeführten Wärme auch Entropie zugeführt wird.

Hierfür gilt:

dS_u = = - m x c_w x dT/T_u

Durch Integration ergibt dies:

S_u(t) = S_u (0) + m x c_w x

Da T(t) ≤ T₀ nimmt S_u mit fortschreitender Zeit monoton zu

(siehe Bild 5).

Die Entropie des Gesamtsystems ist damit:

S(t) = S_u(t) + S_Q(t) = S_u(0) + S_Q(0) + m x c_w x ( - ln )

Und die erzeugte Entropie nach t = ca. 8 h:

S_irr = S(t) – S(0) = Q/T_u – Q/T_m = m x c_w x ( - ln T₀/T(t) ) = 0,153 kJ/K

Schlussbemerkung

Wird ein Teil der zugeführten Exergie als Nutzarbeit genutzt e_Nutz = e_zu – e_V = c (T – T_u) – T_u ((s – s_U) + s_irr), so ergibt sich ein exergetischer Wirkungsgrad von

ξ = e_nutz/e_zu = 1 – e_v/e_zu

Im aufgeführten Beispiel der Abkühlung ohne Exergienutzung:

e_nutz = e_zu – e_v = q x η_c – T_u x s_irr = 356,15 x 0,124 – 288 x 0,153 = 0